The ZK Endgame

Where are we going and what should we be optimizing for?

“It will become recognized that ZK SNARKs are at least as important a technology as blockchains are.” - Vitalik Buterin

Many people have written on the promise of ZK, but few have managed to paint a coherent picture of what the future might look like if ZK fulfills its promise. Similarly it is surprisingly hard to find writings on the trends we are relying on to take us there. This is our attempt at describing the ZK Endgame and in the process clarifying what we need to be optimizing for along the way.

First some honorable mentions. Vitalik Buterin has contributed significantly to popularizing basic ZK concepts and helping people build up an intuition for how these technologies work (1, 2, 3, 4). Wei Dai gave a spectacular talk on “The Cost of Verifiability” which broaches the subject we are discussing. Ingonyama has also done work in this direction with their “ZK Score”. Finally, Polybase Labs maintains ZkBench, a website with benchmarks for different ZK Frameworks, which is very helpful when pondering the types of questions we will explore here.

Why ZK Matters

Traditionally there have been two ways to ensure that a computation was done correctly: trust and re-execution. Whenever someone uses AWS, they are implicitly trusting Amazon to perform the computation correctly. This trust is built on reputation, legal agreements and the law. The other method is re-execution. Instead of trusting a third party, users can run the same computation again themselves and compare the results. This is how blockchains work. Every node in the network runs the same computation to independently verify that the output is correct.

In terms of efficiency, these methods are polar opposites. Trust allows you to minimize redundancy and maximize performance, while re-execution maximizes redundancy and minimizes performance. In other words, traditionally trust has been economically very beneficial and indeed this has been a major contributing factor in the increasing centralization of the internet.

ZK is changing this dynamic, by making it very cheap to verify that a third party performed some computation correctly. This means we can begin to approach the performance and redundancy characteristics of trusted computation without actually needing trust. ZK potentially gives us the best of both worlds.

The ZK Endgame

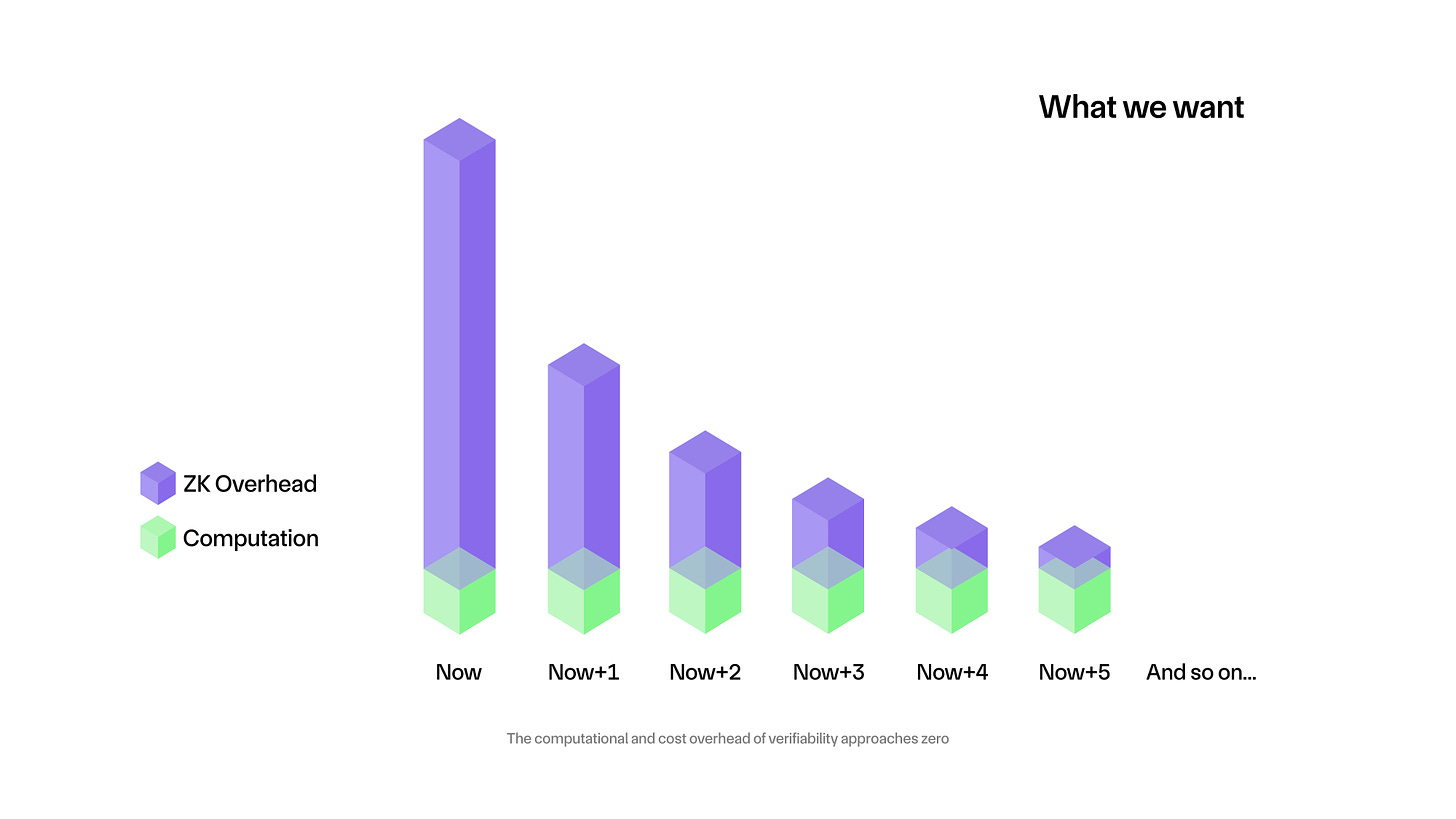
The ZK Endgame can be extrapolated from the “end goal” of ZK, so let's define that first. In our view, the end goal of ZK is for the compute and cost overhead of verifiability to approach zero. Specifically we separate compute and cost overhead, to emphasize that solely a decrease in monetary cost is not sufficient, we also need additional compute time required for ZK to approach zero. Below we will refer to a combination of both measures as just “cost of verifiability”.

Intuitively it seems unlikely that the real cost of verifiability could ever actually be zero, but based on computing trends of the past and present (Moore’s Law, Koomey’s Law, Dennard Scaling, etc), it seems possible that ZK too could get on a trend line which takes it ever closer to zero until we bump against the edges of physics or human ability. It probably goes without saying, but we will likely need many new breakthroughs in cryptography and a lot of new hardware along the way. It’s also possible that when we emerge from the other side, verifiability doesn’t rely on the current ZK mechanisms at all.

This then illuminates the ZK Endgame: what does the world look like if the cost of verifiability approaches zero? For any given computing application there exists some boundary, below which the additional cost for verifiability is justified for that usecase. Furthermore, there exists a global boundary below which the additional cost is so low as to be negligible and thus justified in all usecases. The ZK Endgame begins to unfold as we approach these boundaries.

In fact, we have already crossed the first boundary for the blockchain usecase. Re-execution is so inefficient that even at the current cost of verifiability it is justified to utilize zero-knowledge proofs. However, we suspect the ZK Endgame is only tangentially related to blockchains. As we approach the boundaries for more usecases and hopefully, eventually, the global boundary, we are consistently making it economical and practical for more usecases to not rely on trusted compute. At some boundary you can imagine large companies who rely on Google, Amazon & Microsoft for their business critical compute, to begin requiring proofs alongside their computations. At another, you can imagine citizens demanding that election results be accompanied by a proof that the calculation was made correctly. At the most distant boundary, you can imagine all or most compute globally to come with a proof of execution by default. 

Blockchains then tie into this by removing the last layer of trust. ZK means you don’t need to trust a third party does your computation correctly. Blockchains mean you don’t need to trust that your computation is done at all. In other words, blockchains add censorship resistance, permissionlessness and universal access to the equation.

The ZK Endgame is nothing short of all the world's compute being verifiable or as close to that as is allowed by physics.

Getting to the Endgame

In order to get there, we need to get on a trend line. We think it’s vital to begin tracking the improvements in cost of verifiability over time. This may sound simple, but under the hood it is anything but. Different proof systems make different kinds of compromises, which can be hard to quantify under a banner as simplistic as cost/performance. Similarly, hardware options don’t fit neatly into a performance/cost spectrum, to not even mention the difficulty of estimating the future cost/performance ratios of ASICs and custom chips that are currently being worked on by folks like Fabric, Accseal & Ingonyama. In any real-world application you also need to consider the cost of electricity and bandwidth, both of which fluctuate immensely by region and circumstances. In other words, to make a perfect assessment of the cost of ZK, you may also need to make a perfect prediction of the weather if the energy industry in your region is at the mercy of rainfall or wind.

Perfection, then, is out of reach, but we don’t care about perfection. We care about high level trends. To be able to track high level trends, we need to find metrics for cost of verifiability that are a) simple b) easy to track and c) indicative of underlying progress over time. Here are a couple examples, but we’d invite you to offer others!

Field Sizes

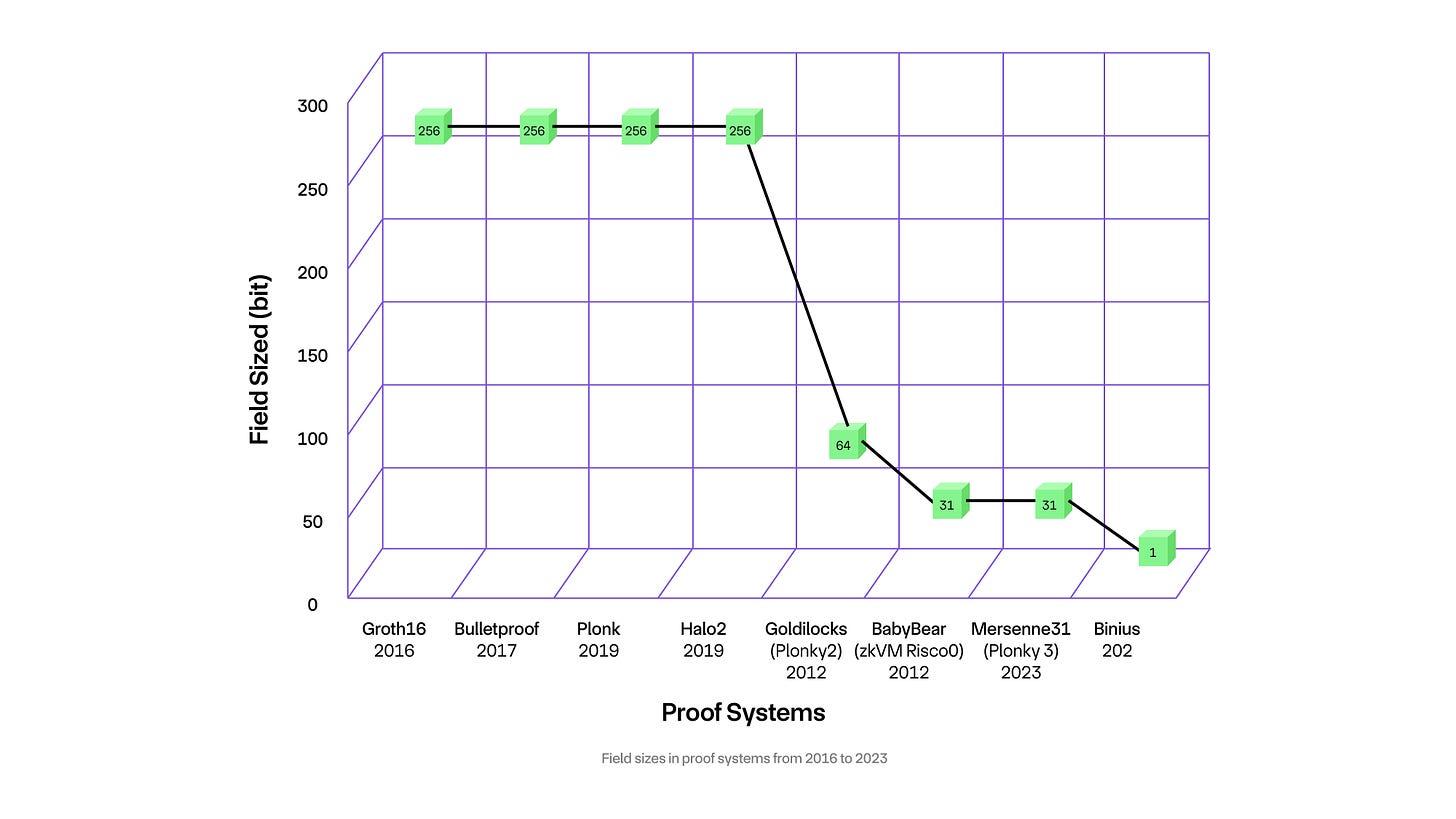
Cryptographic proof systems such as SNARKs and STARKs have evolved significantly to improve computational efficiency. A key component of these systems is the field size, which is a numerical measure related to the underlying mathematical field used in proofs.

The chart below illustrates the progression of field sizes in various proof systems from 2016 to 2023. It's evident that there has been a general trend towards reducing the field size over the years, which is directly correlated with improvements in performance.

In the beginning, most cryptographic proof systems, particularly SNARKs, utilized elliptic curves with a 256-bit field size. While providing robust security, this large field size resulted in complex and resource-intensive computations during the proving process, such as computing quotients, extensions, and random linear combinations. These operations expanded the input data to sizes as large as the field itself, necessitating disproportionately greater computational effort even for small input values.

STARKs initially mirrored the 256-bit field size. However, the introduction of the 64-bit Goldilocks field in systems like Plonky2 in 2022 marked a shift toward smaller fields. Optimized for the native 64-bit arithmetic of commercially available CPUs, Plonky2 dramatically enhanced proving speeds by simplifying arithmetic operations and accelerating data hashing. Nevertheless, such small fields are unsuitable for SNARKs, as they would compromise the security of the elliptic curves.

Further developments in 2023 introduced even smaller field sizes. BabyBear (Risc0 zkVM) and Mersenne31 (Plonky3) both feature 31-bit fields, continuing the trend toward efficiency. The most recent, Binius, uses a 1-bit field size. These systems leverage highly optimized arithmetic operations, particularly in binary fields, which are ideally suited to CPUs, FPGAs, and ASICs, thus enhancing computational speeds.

Verification Cost 

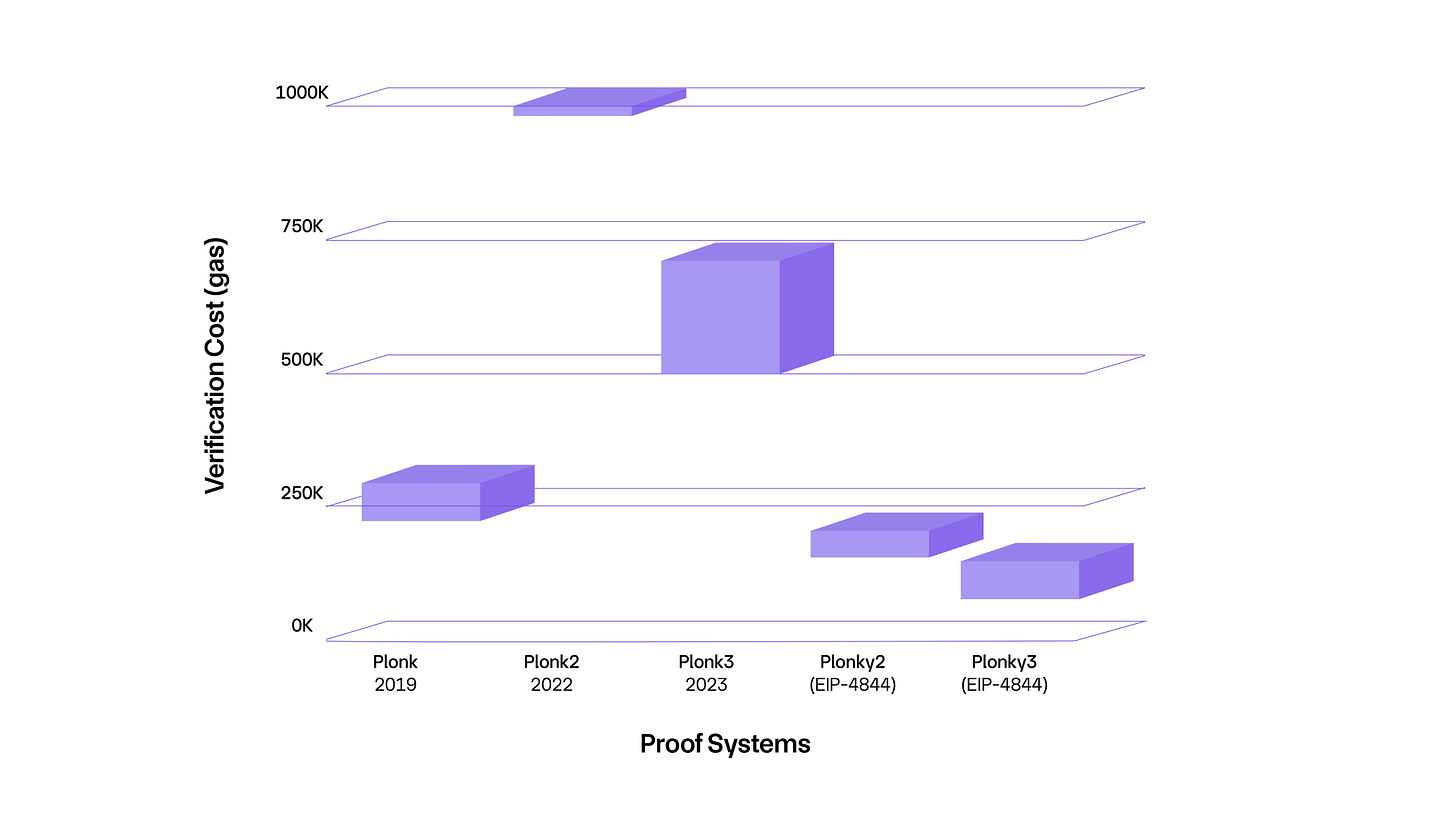
Another crucial metric of proof systems is the cost of verification on Ethereum, which significantly influences the scalability and practical use of blockchain applications. The chart below illustrates the ranges of verification costs for different proof systems.

Introduced in 2019, the Plonk system has a verification gas cost ranging from 223,000 to 290,000 gas. Plonk originates from the SNARK family and employs the KZG commitment scheme, providing a timing advantage.

Plonky2, launched in 2022, utilizes the FRI commitment scheme, a base protocol of STARK that excludes elliptic curves and employs hashing algorithms for polynomial commitments and verification processes. The FRI polynomial commitment offers a significant advantage as it is fully recursive, allowing multiple transaction proofs to be condensed into a single proof, thus streamlining the verification process and reducing costs.

Plonky2 is designed to adjust its proof sizes based on the requirement—using large proofs for speed and smaller proofs for space efficiency. This system adapts its parameters at each recursion step to optimize for specific requirements, fully leveraging the time-space trade-off inherent in the FRI scheme. Starky, working alongside Plonky2, generates transaction-level proofs in parallel, using the same finite field and hash functions. The estimated gas cost for verifying a Plonky2 proof on Ethereum is about 1 million gas, which could decrease to between 170,000 and 200,000 gas with the implementation of EIP-4488.

Plonky3 represents an ongoing effort to enhance cryptographic libraries aimed at accelerating the efficiency of recursive proofs. With continuous development and additional optimizations, Plonky3 is expected to reduce the cost of verification by a factor of 30 to 50 in the coming year, bringing it down to 500,000 - 700,000 gas. With EIP-4488, the cost could be further reduced to between 85,000 and 140,000 gas.

Plonky3 continues to use FRI and aims to support some other polynomial commitment schemes such as Brakedown. It has made improvements to FRI implementation, including optimized data structures, parallel computation to enhance protocol efficiency. 

Despite these advancements, the verification costs for Plonky2 and Plonky3 remain relatively high compared to Plonk. The implementation of EIP-4844, designed to improve data availability and cost efficiency on Ethereum, could significantly reduce the verification costs for these systems, presenting a crucial strategy for the development and optimization of proof systems.

Beyond Basic Metrics

Understanding the development of proof systems requires examining a variety of metrics beyond just field size and verification cost. In-depth analysis should also consider proof size, memory usage, hardware requirements, prover and verifier time, etc., and the impact of these factors on overall system performance.

Over the past 30 years, the ZK field has experienced what can be likened to a Cambrian explosion of cryptographic proofs. This rapid diversification and evolution of proof systems underscore the dynamic nature of cryptographic research and its adaptation to meet changing demands. It demonstrates the industry's efforts to optimize these systems for faster, more efficient computations and cheaper verification costs, while balancing security needs.

As zero-knowledge applications become more mainstream in use, the real-world impact and potential of advanced cryptographic systems will become even more evident. This ongoing evolution is likely to bring more specialized and optimized solutions addressing data privacy and scalability in the blockchain ecosystem and beyond.

The ZkCloud Endgame

At Gevulot we are building the ZkCloud, a decentralized network optimized for offloading arbitrary provable compute. The Gevulot Devnet is now live and free to use for registered users. If you’d like to start offloading provable compute or, for example, start benchmarking proof systems to help the industry build on the narrative we’ve laid out, you can do so right now, by registering a key.

Learn more about Gevulot:
Website | Docs | GitHub | Blog | X (Twitter) | Galxe Campaign | Telegram | Discord